General Concepts
Dernière mise à jour
Dernière mise à jour
K2 Geospatial 2024
The API of JMap geometries is used for development purposes in JMap Pro and JMap Server.
In JMap, all vector data elements that appear on the map are based on geometries. They are simple classifications of basic geometric elements such as points, lines, and surfaces. In JMap, the classification scheme of geometries has been largely inspired by the model of geometries published by the Open Geospatial Consortium. Geometries do not contain attributes, identifiers, or display properties, but only two-dimensional x and y coordinates.
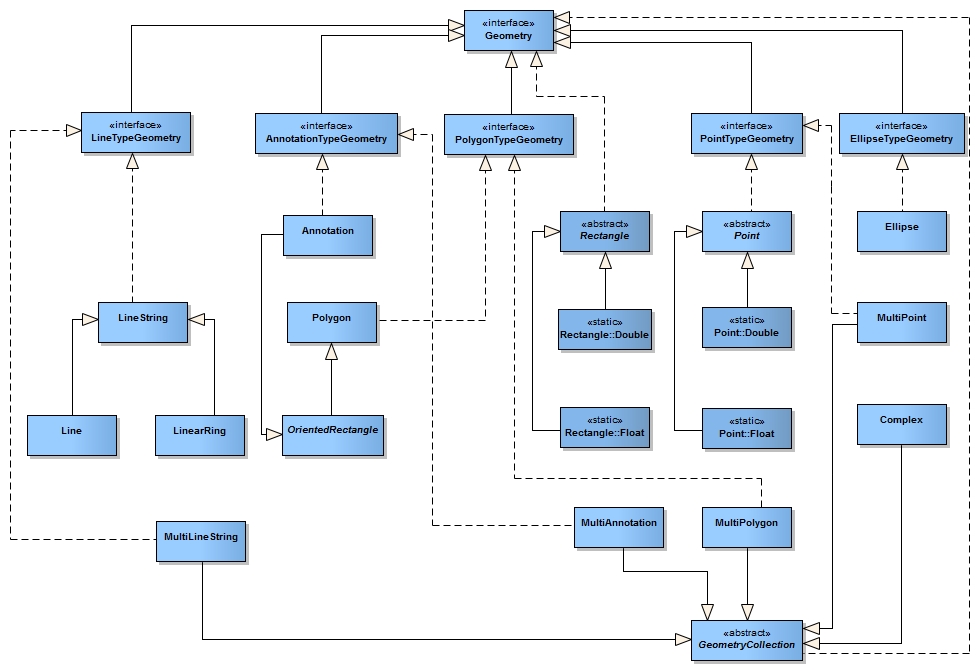
In JMap, the geometry classes can be found in the com.kheops.jmap.spatial package. The interface implemented by all geometries is Geometry.
The Point is a type of basic geometry used to compose all geometries. This type of geometry only contains a set of coordinates (x,y). This class is abstract and, therefore, its derivatives - Point.Float (simple precision) and Point.Double (double precision) - must be used.
// Creating a new point specifying coordinates Point pt1 = new Point.Double(-73., 45.);
// Creating a new point by cloning an existing point Point pt2 = (Point) pt1.clone();
// Changing the location of an existing point pt1.setLocation(-74., 45);
The main geometry classes are the following:
Composite versions of geometries exist to support collections of geometries of the same type. These classes are: MultiPoint, MultiCurve, MultiLineString, MultiSurface and MultiPolygon. In addition, the Complex class is a special type of collection comprising various types of geometries.
To simplify the management of all these types of geometries, 5 interfaces are available: PointTypeGeometry, LineTypeGeometry, PolygonTypeGeometry, AnnotationTypeGeometry and EllipseTypeGeometry. These interfaces combine all types of geometries, including collections.
JMap allows you to create single precision or double precision geometries. Combined with other strategies, simple precision is mainly used to compress data in order to optimize system performance. As a programmer, you should only use double precision.
// Creating a new point with single precision Point pt1 = new Point.Float(-73., 45.);
// Creating a new point with double precision Point pt2 = new Point.Double(-73., 45.);
Spatial operators are used to make geometric calculations on the geometries. These calculations can generate 3 types of results:
Numeric results (e.g. calculate the distance between 2 geometries)
Boolean results (e.g. test to see if 2 geometries intersect)
Geometric results (calculate the union of 2 geometries)
The GeometryUtil class provides simple methods to perform calculations on geometries. The methods most often used are presented in the following table:
The PrecisionModel interface allows you to define the tolerance being considered in performing calculations using the geometries. Using a precision model that is well adapted to the geometries can give more precise results when making calculations.
The precision model generally varies according to the measurement unit of the data (meters, degrees, etc.). The PrecisionModelFactory class allows you to obtain an instance of PrecisionModel for a given unit. Each instance of the Layer class has its own instance of PrecisionModel that can be used. It is also possible to ask JMap to determine the optimal precision model for a specific geometry.
The following example shows different ways of generating an appropriate precision model.
// Obtain the optimal precision model for data of the current projectProject project = ... PrecisionModel precisionModel1 = PrecisionModelFactory.getInstance(project.getMapUnit());
// Obtain the optimal precision model for unit Meter PrecisionModel precisionModel2 = PrecisionModelFactory.METER;
// Obtain the optimal precision model of a layerLayer layer = ... PrecisionModel precisionModel3 = layer.getPrecisionModel();
// Obtain the optimal precision model for the specified geometry Geometry geometry = ... PrecisionModel precisionModel4 = PrecisionModelFactory.getInstance(geometry);
You can perform transformations of all sorts on geometries. The Geometry interface contains the method transform(Transformation), which receives an instance of Transformation. This method creates a clone of the geometry, applies the specified transformation on it and returns the newly transformed geometry. Transformations can change the coordinates of the geometry and even modify the nature of the geometry itself. They can be used to apply a map projection or a generalization to geometries, for instance.
It is also possible to apply transformations using the transform() method of the Transformation class. In this case, the geometry may not always be cloned, depending on the type of transformation. Refer to the documentation of each transformation for more information.
The UnaryTransformation class is the base class of the transformations that only modify the coordinates composing the geometry. If you must implement your own transformation class, you will probably derive it from this class.
The following table shows the transformations that are available with the JMap API.
The following code example shows how to use the precision change transformation.
Point[] points = new Point[]
{
new Point.Double(10., 10.),
new Point.Double(20., 20.),
new Point.Double(30., 30.)
};
LineString doubleLineString = new LineString( points );
// The transformation can be done by the geometry. After the execution, doubleLineString will still contain single precision coordinates.
LineString singleLineString1 = (LineString)doubleLineString.transform(PrecisionTransformation.TO_FLOAT);
// The transformation is made directly on the geometry. After the execution, doubleLineString will contain single precision coordinates. Moreover, singleLineString2 refers to the same instance as doubleLineString.
LineString singleLineString2 = (LineString)PrecisionTransformation.TO_FLOAT.transform(doubleLineString);
The following code example shows how to use the map projection change transformation.
Point[] points = new Point[] { new Point.Double(-73.12345, 45.12345), new Point.Double(-73.54321, 45.54321) }; LineString lineString = new LineString( points );
// Define the source and the destination projections Projection fromProjection = new LongitudeLatitude(); Projection toProjection = new Mtm(); toProjection.setParams("8"); // zone 8 // Create a combined projection object that converts points from one projection to the other final CombinedProjection combinedProj = new CombinedProjection(fromProjection, toProjection); // Apply the projection transformation lineString = (LineString)lineString.transform(new ProjectionTransformation(combinedProj));
The following example shows how to create an anonymous transformation class using the adapter TransformationAdapter. The transformation converts the points into ellipses.
Point[] points = new Point[]
{
new Point.Double(10., 10.),
new Point.Double(20., 20.),
new Point.Double(30., 30.)
};
// Create a new transformation which creates a new ellipse at the specified location. Transformation tr = new TransformationAdapter()
{
public Geometry transform(Point point)
{
return new Ellipse(
(Point)point.clone(),
new Dimension.Double(5, 3), 0
);
}
};
// Apply the transformation on all points
Ellipse[] ellipses = new Ellipse[points.length];
for (int i = 0; i < ellipses.length; i++)
ellipses[i] = (Ellipse)tr.transform(points[i]);
The bounding rectangle (MBR for Minimum Bounding Rectangle) of a geometry is the smallest orthogonal rectangle that totally encompasses the geometry. The MBR is used in JMap to do quick spatial analyses of a large number of geometries before using more precise (yet slower) algorithms on a smaller number of geometries. As prescribed by the Geometry interface of JMap, all types of geometries implement the getBounds() method that generates the MBR of the geometry.
The MBR of a point is a rectangle with a width of 0 and a height of 0. The MBR of a vertical line is a rectangle with a width of 0 and the MBR of a horizontal line is a rectangle with a height of 0.
Geometry classes
x,y coordinates used to compose all other geometries.
Abstract type from which all linear geometries are derived (Line, LineString, etc.).
Simple line defined by two points.
A line with several parts. Composed of N nodes and N-1 segments.
A Line String where the first and last nodes are equal. Forms a closed loop.
Abstract type from which all surface geometries (rectangle, polygon, etc.) are derived.
Polygon composed of one exterior LinearRing and of 0, 1 or several LinearRings that are holes.
Non-oriented rectangular surface (horizontal and vertical sides)
A rectangular surface that can be oriented.
Ellipse composed of a central point, an a radius and a b radius.
Derived from OrientedRectangle, the Annotation class defines the extent of a message to be displayed on the map.
Spatial relation tests (boolean)
Test to determine if the first geometry contains the second geometry. The order of the geometries is important.
Test to determine if the first geometry crosses the second geometry. The order of the geometries is important.
Test to determine if the first geometry is disjointed from the second geometry. The order of the geometries is important.
Test to determine if the two geometries intersect. The order of the geometries is not important.
Test to determine if the two geometries overlap. The order of the geometries is not important.
Test to determine if the two geometries possess the spatial relationships defined in the parameter matrix. The order of the geometries is important. For more information, refer to http://en.wikipedia.org/wiki/DE-9IM.
Test to determine if the two geometries are spatially equal (all the coordinates are identical). The order of the geometries is not important.
Test to determine if the two geometries touch each other. The order of the geometries is not important.
Test to determine if the first geometry is within the second geometry. The order of the geometries is important.
Geometry operations resulting in new geometries
Returns a geometry that represents a buffer zone around the specified geometry. The size of the zone is specified as a parameter.
Returns a convex geometry created from the specified geometry.
Returns the geometry resulting from the difference between the first and second geometries. The order of the parameters is important.
Returns the geometry resulting from the symmetrical difference between the two geometries. The order of the parameters is not important.
Returns the geometry resulting from the intersection of the two geometries. The order of the parameters is not important.
Returns the geometry resulting from the intersection of all geometries passed as parameters. The order of the parameters is not important.
Returns the geometry resulting from the union of the two geometries. The order of the parameters is not important.
Returns the geometry resulting from the union of all geometries passed as parameters. The order of the parameters is not important.
Calculations
Calculates the shortest distance separating both geometries. The order of the parameters is not important.
Applies the projection specified in the constructor's parameters to a geometry. The projection can also be applied in reverse.
Applies an x and y translation to a geometry, as specified in the constructor's parameters.
Applies a generalization to a geometry, according to the tolerance specified in the constructor's parameters.
Transforms a double precision geometry into a single precision geometry.
Transforms a single precision geometry into a double precision geometry.
